6. ニューラルネットワーク#

本章では，DDPGの関数近似で用いられるニューラルネットワークの詳細やPythonプログラムでの扱い方を紹介します．

6.1. 基本的な構造#

DDPGなどの強化学習では，一般的に非常にシンプルなニューラルネットワークネットワークが用いられます． ニューラルネットワークでは，関数への入力\(x\)に対して，層と呼ばれる関数の構造を複数回適用します．

以下，入力を\(x \in \mathbb{R}^n\)，出力を\(y \in \mathbb{R}^m\)とする， 単層のニューラルネットワークの式を示します．

\[ y = g(xW+b),\ W \in \mathbb{R}^{n \times m}, b \in \mathbb{R}^{1 \times m} \]

ここで関数\(g:\mathbb{R} \rightarrow \mathbb{R}\)は 活性化関数 と呼ばれる非線形関数であり， 引数がベクトルや行列の際は各要素ごとに適用されます．

また，2層ニューラルネットワークは，以下の式で表されます．

\[\begin{split} h = g^{(0)}(xW^{(0)}+b^{(0)}),\\ y = g^{(1)}(hW^{(1)}+b^{(1)}). \end{split}\]

これらを繰り返すことにより，多層ニューラルネットワークを構成することが出来ます． 多層ニューラルネットワークにおいては， 入力に近い層を 入力層 ， 出力に近い層を 出力層 ， 中間的な層を 中間層 と呼びます．

ニューラルネットワークは様々な関数を近似する表現能力を有しています．

6.2. ニューラルネットワークの最適化#

ニューラルネットワークで構成された関数\(y=f(x;\omega)\)を考えます． ここで\(x\)は入力で\(y\)は出力，\(\omega\)はパラメータを表します． このニューラルネットワークに対して，何かしらの損失関数というものを考えます． 例えば，\(y=f(x;\omega)\)で\(\mathcal{D} = \{(\hat{x}_0,\hat{y}_0),(\hat{x}_1,\hat{y}_1),\cdots,(\hat{x}_k,\hat{y}_k)\}\) というデータを近似したいと考えると，以下のような損失関数を考えることが出来ます．

(6.1)#\[ L(\omega;\mathcal{D}) = \frac{1}{|\mathcal{D}|} \sum_{n=0} \left( \hat{y}_n - f(\hat{x}_n;\omega) \right)^2 \]

また，損失関数のパラメータ\(\omega\)に対する勾配\(\nabla_\omega L(\omega;\mathcal{D})\)が分かれば， 勾配ベースの手法により，この関数を最小化することができます．

ここでは，詳細は説明しませんが， ニューラルネットワークフレームワークと呼ばれる，ニューラルネットワークを扱うプログラムの多くは， 自動微分(Automatic Differentiation) と呼ばれる機能を提供しています． これを用いるとプログラムで構成された式(例えば式(6.1)など)に対する勾配を自動的に計算できます．

また，それら勾配を用いて勾配ベースの手法により， 損失関数を最適化するツールも提供されています．

6.3. 実装#

本節では，実際にニューラルネットワークの一種である PyTorch を用いて，

  1. ニューラルネットワークを構成

  2. 損失関数を設定

  3. 損失関数の最小化

という流れの実装を行っていきます．

import torch
from torch import nn
from torch import optim
import torch.nn.functional as F
import matplotlib.pyplot as plt

本節では，入力/出力ともに1次元の，3層のニューラルネットワークを構成してみます． ネットワークを式で表すと以下のようになります．

\[\begin{split} h^{(0)} &= \text{ReLU}(xW^{(0)}+b^{(0)}),\\ h^{(1)} &= \text{ReLU}(h^{(0)}W^{(1)}+b^{(1)}),\\ y &= h^{(1)}W^{(2)}+b^{(2)}. \end{split}\]

各パラメータの次元は以下のようになります．

\[\begin{split} &W^{(0)} \in \mathbb{R}^{1 \times 256}, b^{(0)} \in \mathbb{R}^{256}, h^{(0)} \in \mathbb{R}^{256} \\ &W^{(0)} \in \mathbb{R}^{256 \times 256}, b^{(0)} \in \mathbb{R}^{256}, h^{(0)} \in \mathbb{R}^{256} \\ &W^{(0)} \in \mathbb{R}^{256 \times 1}, b^{(0)} \in \mathbb{R}^{1}, h^{(0)} \in \mathbb{R}^{1} \end{split}\]

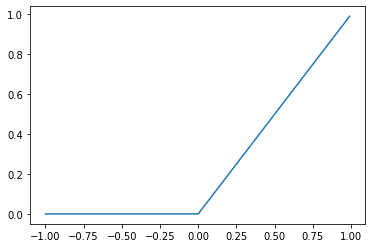
ここで，\(\text{ReLU}(\cdot)\)は，活性化関数であり，入力と出力の関係は以下グラフのようになります．

x = torch.arange(-1, 1, 0.01)
y = F.relu(x)
plt.plot(x, y)
plt.show()
../_images/02nn_3_0.png

このネットワークをクラスで実装すると以下のようになります．

class Network(nn.Module):  ## nn.Moduleを継承
    def __init__(self) -> None:
        super().__init__()
        # 各層を初期化
        self.linear0 = nn.Linear(1, 256)
        self.relu0 = nn.ReLU()
        self.linear1 = nn.Linear(256, 256)
        self.relu1 = nn.ReLU()
        self.linear2 = nn.Linear(256, 1)

    def forward(self, x):
        """入力から出力を計算する関数"""
        h0 = self.relu0(self.linear0(x))  # 入力層
        h1 = self.relu1(self.linear1(h0))  # 中間層
        y = self.linear2(h1)  # 出力層
        return y


f = Network()
print(f)

Network(
  (linear0): Linear(in_features=1, out_features=256, bias=True)
  (relu0): ReLU()
  (linear1): Linear(in_features=256, out_features=256, bias=True)
  (relu1): ReLU()
  (linear2): Linear(in_features=256, out_features=1, bias=True)
)

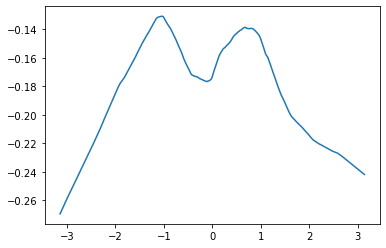
このネットワークをプロット\(x \in [-\pi,\pi]\)の範囲すると，以下のようになります．

x = torch.arange(-torch.pi, torch.pi, 0.01)[..., None]
y = f(x)
plt.plot(x.detach().numpy(), y.detach().numpy())
plt.show()
../_images/02nn_7_0.png

この関数を

\[y = sin(x)\]

にフィッティングすることを考えます．

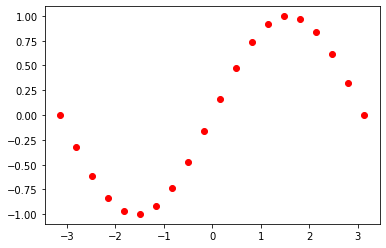
教師データを 20 個生成し，それに対する平均二乗和誤差を計算する関数を実装します．

# 教師データを生成
x_t = torch.linspace(-torch.pi, torch.pi, 20)[..., None]
y_t = torch.sin(x_t)

plt.scatter(x_t, y_t, color="red")
plt.show()
../_images/02nn_9_0.png 
# 損失関数を計算
def compute_loss(f: Network):
    # yの予測値を計算
    y_pred = f(x_t)

    # 平均二乗和誤差を計算
    loss = F.mse_loss(y_pred, y_t)
    return loss


print(compute_loss(f))

tensor(0.5223, grad_fn=<MseLossBackward0>)

最適化器を用意します． 本稿では強化学習でよく用いられる Adam という最適化手法を用います．

optimizer = optim.Adam(f.parameters(), lr=1e-3)  # 引数に最適化対象のパラメータと学習率を与える

それでは，これらを用いて，100ステップ最適化を行います．

for i in range(100):
    loss = compute_loss(f)  # 損失を計算
    optimizer.zero_grad()  # 保存されている勾配情報を初期化
    loss.backward()  # 損失のパラメータに対する勾配を計算
    optimizer.step()  # 1ステップ最適化する

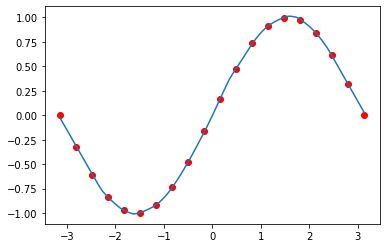
結果をプロットすると以下のようになります．

x = torch.arange(-torch.pi, torch.pi, 0.01)[..., None]
y = f(x)
plt.plot(x.detach().numpy(), y.detach().numpy())
plt.scatter(x_t, y_t, color="red")
plt.show()
../_images/02nn_16_0.png