1. 強化学習が対象とする問題#

\[\DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \newcommand{\E}{{\mathrm E}} \newcommand{\underE}[2]{\underset{\begin{subarray}{c}#1 \end{subarray}}{\E}\left[ #2 \right]} \newcommand{\Epi}[1]{\underset{\begin{subarray}{c}\tau \sim \pi \end{subarray}}{\E}\left[ #1 \right]}\]

1.1. マルコフ決定過程#

強化学習は学習主体が制御対象との相互作用をもとに学習し，目標を達成するための枠組みです．学習主体は エージェント(Agent) と呼ばれ，制御対象は 環境(Environment) と呼ばれます．制御対象の環境は，一般的に マルコフ決定過程(Markov decision process; MDP) で定式化されます．マルコフ決定過程は\((\mathcal{S}, \mathcal{A}, p, r, p_0)\)で定義され，以下に各要素を列挙します．

有限状態空間(State Space): \(\mathcal{S} \ni s\)
有限行動空間(Action Space): \(\mathcal{A} \ni a\)
状態遷移確率分布関数: \(p: \mathcal{S} \times \mathcal{S} \times \mathcal{A} \rightarrow [0, 1]\):

\(p(s'|s, a) := \Pr(S_{t+1} = s'| S_{t} = s, A_t = a),\ \ \ \forall t \in \mathbb{N}_0.\)
報酬関数(Reward Function): \(r: \mathcal{S} \times \mathcal{A} \rightarrow [r_{\text{min}}, r_{\text{max}}]\)
初期状態確率分布関数(Initial State Distribution): \(p_0: \mathcal{S} \rightarrow [0, 1]:p_0(s) := \Pr(S_0 = s)\)

マルコフ決定過程の簡単なイメージを以下の図に示します．

OpenAI Spinning Upより

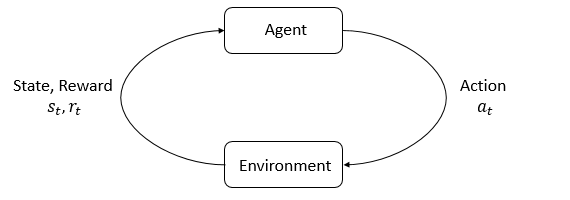
ここで重要なことは状態遷移確率分布関数の形が\(p(s'|s, a)\)となっており，これは次時刻の状態が現在の状態と行動にのみ依存しているという点です．このような確率過程の性質をマルコフ性といいます．

1.1.1. 終了状態#

強化学習が対象とするタスクには 終了状態(Terminal state) が設けられている場合があります．この終了状態にエージェントが到達するとタスクが終了したとみなされ，その後報酬を獲得することはありません．例えば，レーシングゲームにおいて，ゴールに到達した状態は終了状態であると言えます．また，スタートから終了までの一連の流れを エピソード(Episode) と呼び，エピソードが存在するタスクを エピソードタスク(Episodic Tasks) と呼びます．

エピソードタスクとは違い，終了状態が存在しないタスクもあります．このようなタスクは 連続タスク(Continuing Tasks) と呼ばれます．

1.2. 方策#

マルコフ決定過程への入力となる行動を決定するルールである 方策(Policy) を定義します．方策とは，環境から観測した状態\(s\)に対して，エージェントがどのような行動\(a\)を選択するかの規則を表すものです．方策には様々な形のものがありますが，本書では 確率的方策(Stochastic policy) \(\pi : \mathcal{A} \times \mathcal{S} \rightarrow [0,1]\) と 決定的方策(Determinstic policy) \(\mu : \mathcal{S} \rightarrow \mathcal{A}\) の 2 種類を取り扱います．確率的方策は，ある状態のもとである行動を選択する確率を表す条件付き確率\(\pi(a|s) := \text{Pr}(A=a, S=s)\)で定義され，行動は以下の様にサンプルされます．

\[a \sim \pi(\cdot|s)\]

一方，決定的方策は，ある状態のもとで選択する行動を表す関数で表され，行動は以下のように決定されます．

\[a = \mu(s)\]

このように，選択する行動が過去の状態に依存しない方策を マルコフ方策 といい，時間ステップに依存しない方策を 定常方策 といいます．本書では特に断りがない限り定常マルコフ方策を扱います．

実用上方策は，関数近似(e.g. 線形近似，多項式近似，ニューラルネットワーク)によりパラメータ\(\theta\)で近似した関数\(\theta\)し\(\pi_\theta, \mu_\theta\)で表される場合や，状態・行動空間が離散的で少ない場合は，状態行動対に対応する確率や，状態に対応す行動を全て保持する表(tabular)で表される場合があります．

1.3. 評価関数#

環境や方策に対して，強化学習は一般的に目的関数と呼ばれる方策を評価する関数を定義し，それを最大化する方策を求める問題と言えます．評価関数には様々な形のものが考えられますが，典型的には， 期待報酬(expected reward)

(1.1)#\[J(\pi) =\underE{\pi}{\lim_{T \rightarrow \infty} \frac{1}{T}\sum_{t=0}^{T} R_t }\]

や 期待割引累積報酬(expected discounted cumulative reward)

(1.2)#\[J(\pi) = \underE{\pi}{\lim_{T \rightarrow \infty} \sum_{t=0}^{T} \gamma^t R_t }\]

が用いられます．ここで，\(\gamma \in [0,1)\)は割引率と呼ばれるパラメータです．マルコフ過程が時間的に無限に続く際，累積報酬を有限の値に収める役割があります．\(\gamma\)が 1 に近いほど，長期的な報酬和を考慮することを，0 に近いと短期的な報酬を重視することを意味します．

本書では，より一般的に用いられる期待割引累積報酬を主に扱います．また今後，確率変数である(時刻 t からの)累積割引報酬を以下のように表記します．

(1.3)#\[G_t = R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots = \lim_{T \rightarrow \infty} \sum_{k=t}^{T} \gamma^{k-t} R_k\]

この表記により，期待割引累積報酬を\(J(\pi) = \underE{\pi}{G_0}\)と書き表せます．

You should know

評価関数が定義されたので，最適方策は評価関数を最大化する方策\(\argmax_{\pi}J(\pi)\)であると考えるかもしれません．しかし，厳密な最適方策の定義は評価関数の最大化のみではありません．評価関数を最大化することは必要条件ではありますが十分条件であるとは限らないのです．(マルコフ過程がエルゴード性を満たす場合は必要十分となる) 詳しくは次章以降に示します．

1.4. プログラムによるシミュレーション#

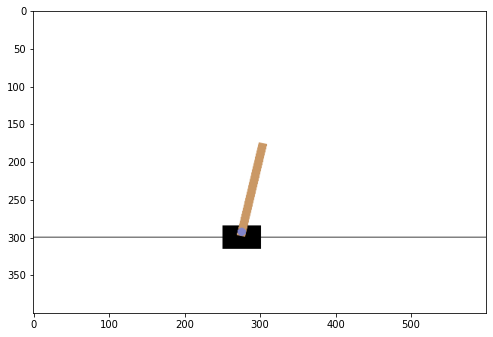
本節では，強化学習が対象とする問題のシミュレーションを行います．シミュレーションには Python ライブラリの一つであるOpenAI Gymを用います．このライブラリには，様々な環境が実装されているのですが，今回は基本的な問題の一つであるCart Poleを用います．

この問題で行動は，0:cart を左に押す/1:cart を右に押す，の二種類で，状態は cart の位置/速度，pole の角度/角速度を表す 4 次元の実数値ベクトルとなります．報酬は pole が倒れていなかったら各時間ステップで 1 得られます．

以下のプログラムは，

方策を，状態に関わらずランダムな行動を選択する確率的方策
評価関数を，\(\gamma = 0.99\)とした際の累積割引報酬

とした際のシミュレーションです．

import gnwrapper
import gym


env = gnwrapper.LoopAnimation(gym.make("CartPole-v1"))  # 環境を作成

# 状態に関わらずランダムな行動を選択する方策
def policy(state):
    return env.action_space.sample()


gamma = 0.99  # 割引率
r_sum = 0  # 割引累積報酬
t = 0  # 時刻ステップ

state = env.reset()  # 初期化

while True:
    action = policy(state)  # 状態から行動を選択
    next_state, reward, done, info = env.step(action)  # 行動を実行して(次の状態，報酬，終了判定，その他情報)を観測

    r_sum += (gamma**t) * reward

    env.render()  # 描画

    state = next_state  # 状態を更新
    if done:
        break

print(f"Discounted Cumulative Reward : {r_sum}")

env.display()

/home/hisaki/workspace/rl-semi/.venv/lib/python3.8/site-packages/gym/utils/passive_env_checker.py:97: UserWarning: WARN: We recommend you to use a symmetric and normalized Box action space (range=[-1, 1]) https://stable-baselines3.readthedocs.io/en/master/guide/rl_tips.html
  logger.warn(

Discounted Cumulative Reward : 12.0

強化学習新人ゼミ2022

強化学習が対象とする問題

Contents